Options 101 – Your Guide to Trading Options

1.    Option Basics

1.1. What are Options?

An option is a contract between two parties – the option writer (seller) and the option holder (buyer) – that gives the holder of the option the right to buy (or sell) the underlying from (to) the option writer.

It is a right and NOT an obligation for the option holder to exercise the option. There are two types of options – calls and puts.

Call Options

The call option buyer has the right but not obligation to buy the underlying asset at the strike price within a specific period of time. If the option holder decides to exercise the call option, he will have to pay the seller the strike price.

Put Options

The put option buyer has the right but not obligation, to sell the underlying asset at the strike price.

1.2. Terminologies

Strike Price

The closer the strike price is to the underlying asset value, the more valuable the option because the odds are better that the option will expire with a positive intrinsic value (in-the-money).

The call option buyer will typically exercise the option when the asset price rises above the strike price:
Current Market Price ‒ Option Strike Price > 0

 

The put option buyer will exercise when the asset price falls below the strike price:
Option Strike Price ‒ Current Market Price > 0

 

Expiration Date

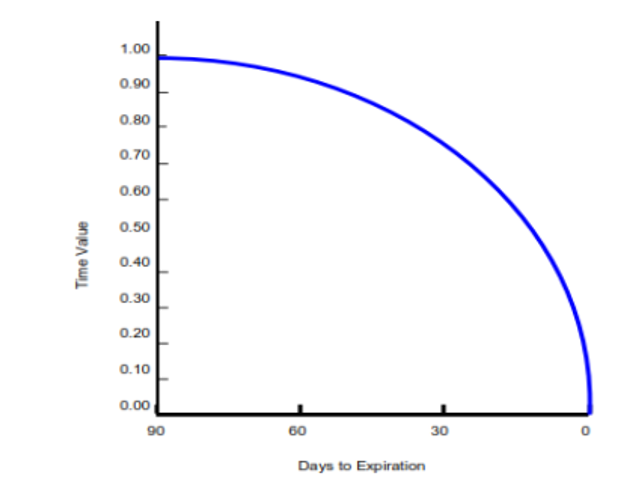
All options will have a maturity date or expiration date. The longer the time to maturity, the higher the time value.

Style of Option

Options are either European-style or American-style options.

European options can only be exercised on the expiration date, while American options can be exercised at any time before expiration

 

1.3. Moneyness, Time Value, and Implied Volatility

Intrinsic Value- Moneyness:

Intrinsic value is the potential profit or loss of the option when an option buyer exercises it at a point in time. It is also referred to as “Moneyness”.

As the option holder has the right but not the obligation to buy or sell the underlying asset, the intrinsic value of an option cannot be negative.

• Intrinsic Value of a Call Option = Max (0, Current Market Price of Underlying ‒ Strike Price)
• Intrinsic Value of a Put Option = Max (0, Strike Price ‒ Current Market Price of Underlying)

An option has intrinsic value when there are profits– when it is in-the-money (ITM).

When an option is at-the-money (ATM) or out-of-the-money (OTM), the intrinsic value is zero.

How does Option Moneyness affect its Price (premium)?

• Typically, ITM options have higher premiums as the option can already be exercised and is profitable.
• ATM options have premiums that are lower than ITM but higher than OTM
• OTM options have the lowest premiums as there is a higher likelihood for the option to expire worthless.
  
  

Source: Bloomberg, Nvidia Option Monitor, 25 June

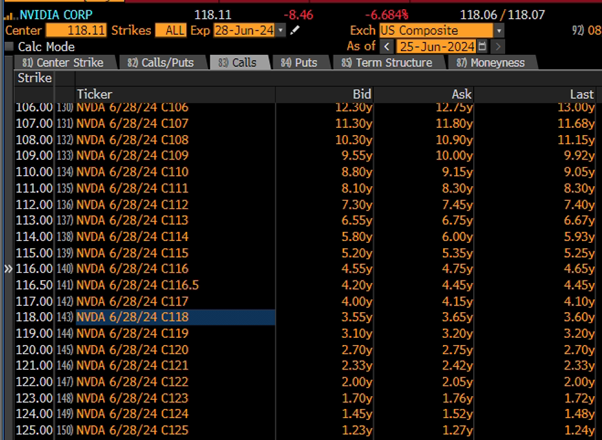
As seen above, denoted by the “Ask” column, given that the asset price of Nvidia is 118.11, option premiums for Nvidia call options are higher when the strike price is below 118 (ITM), while premiums are lower when the strike price is above 118 (OTM).

Option Price (Premium):

The option price that the option buyer pays to the seller is also commonly called the option premium.

An option’s total premium is based on its intrinsic plus extrinsic value. A key part of extrinsic value is known as “time value.”

• Option Price = Intrinsic Value (“Moneyness”) + Extrinsic Value (Time Value & Implied Volatility)

 

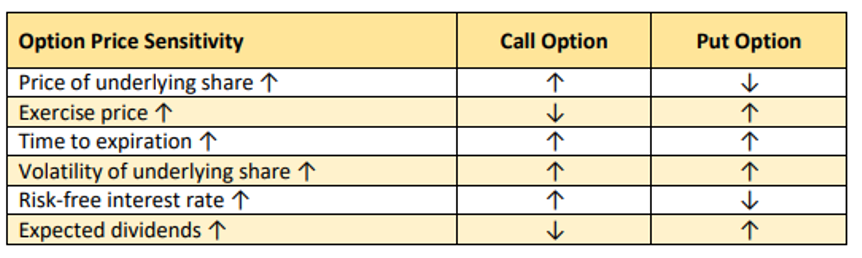
Factors Influencing Option Prices (Premiums)

There are six major factors which affect the price of equity options:

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

Time Value of Options:

The option price is generally higher than its intrinsic value before expiry.

• Time Value of Option = Option Price – Intrinsic Value

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

 

• The longer the time to maturity, the greater the time value of the option, as the option writer requires greater compensation (premium) for the higher likelihood of the underlying moving in favour of the option holder.
• Time value decreases as it approaches expiry because there’s less time for the underlying security to move favourably.

At expiry, time value will be zero. The value of the option at expiration is exactly its intrinsic value:

• Option Price = Intrinsic Value (as Time Value → 0)

Implied Volatility (IV):

Another factor that affects extrinsic value and time value is implied volatility (IV).

Implied Volatility – measures how much the market expects asset prices to move for an option price (the volatility that is implied by the market).

Generally, higher IV suggests higher option prices because there is a higher chance for the underlying asset price to move in favour of the option buyer and be in-the-money.

Option Greeks:

Option Greeks are statistical values that drive option prices and describe its sensitivity to various risk parameters:

1. Delta – Change in option price vs change in the price of the underlying asset.
2. Gamma – Change in delta vs change in the price of the underlying asset.
3. Theta – Change in option price vs change in time to maturity.
4. Vega – Change in option price vs change in volatility.
5. Rho – Change in option price vs change in interest rates

Do look forward to our follow-up reports to find out more regarding Option Greeks!

 

2. Option Payoff Profiles

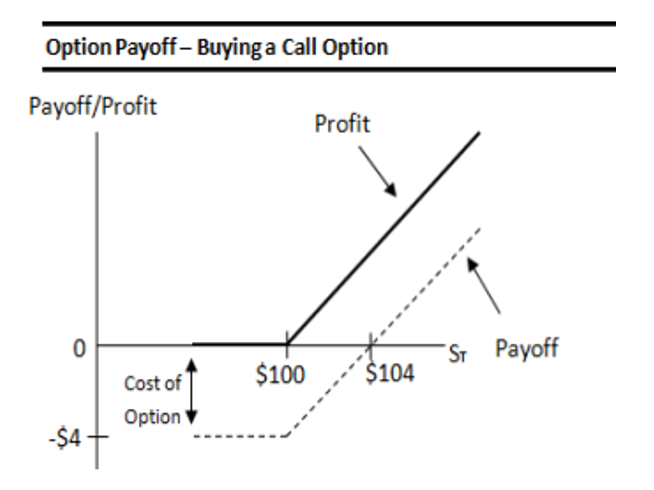
2.1 Long Call Option:

As an example, recall that Calls are only exercised when ST>X

• Call Premium (c) = $4
• Strike Price (X) is $100
• The underlying asset price (ST) is $110

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

 

Payoff (C) & Profit to Call Buyer:

• ST > X, In-the-money: Payoff (C) = ST – X,
• if ST = X, At–the-money: C = 0
• if ST < X, Out-of-the-money: C = 0

Profit: Payoff – premium= $110- $100- $6= $4

Breakeven: The call option holder only breaks even if the price of the underlying asset rises above the exercise price by an amount equal to the price of the option (premium).

Breakeven: when ST= $100 + $4

Maximum gain: Payoff – Premium, can theoretically be unlimited.

Maximum loss: Max loss is option premium, call payoff cannot be negative. If option holder does exercise the option, it expires worthless.

2.2. Short/Write Call Option:

• Premium is $4 (c)
• The option’s exercise price (X) is $100
• Current underlying asset price (S) is $90

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

 

Payoff to Call Writer/Seller:

• If ST < X, In-the-money: C = – (ST – X)
• if ST ≥ X, At–the-money/ Out-of-the-money: C = 0

Profit: Maximum profit is limited to the premium of $4, as long as the option is OTM.

Breakeven: The breakeven point for both the call option buyer and writer is exactly the same, i.e., $104.

Maximum loss: The maximum loss for a call option writer is, theoretically, unlimited. The higher the underlying asset price, the greater the loss to the option writer.

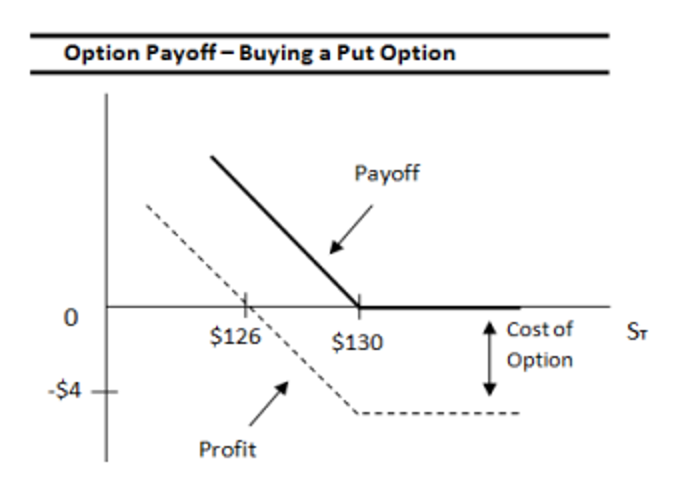
2.3. Long Put Option:

Recall that Puts are exercised only when ST<X

• Premium (p) is $4
• The option’s exercise price (X) is $130
• The underlying asset price (ST) at expiry is $120
  
  

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

 

Payoff (P) to Put Buyer:

• if X > ST, ITM: Payoff (P) = X – ST
• if ST = , ATM: P = 0
• if X < ST, OTM: P = 0

 

Profit: The payoff to the put option buyer is X – ST – premium = $130 – $120 – $4 = $6.

Breakeven: The put option holder only breaks even if the price of the underlying asset falls below the exercise price by an amount equal to the option premium.

Breakeven= X – p= $126

 

Maximum Gain: P- premium, $130 – $4 = $126.

Maximum Loss: maximum loss is the option premium paid of $4.

 

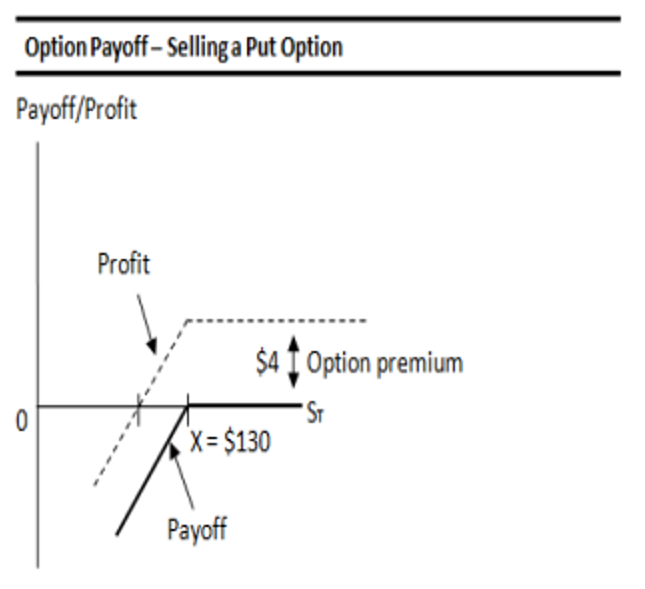
2.4. Short/Write Put Option:

• Option premium = $4
• The option’s exercise price X is $130
• Current value of the asset is ST1 = $140
• Value of underlying asset at expiry is ST2 = $120

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

 

Payoff to Put Seller / Writer:

• If ST < X (In-the-money): P = – (X – ST)
• If ST ≥ X (At–the-money/Out-of- the-money): P = 0

Breakeven: Same for both the put option buyer and put option write.

Profit: Premium of $4 is the maximum profit.

Maximum Loss: The maximum loss is when the underlying asset price falls to zero.

3. Basic Option Strategies

3.1. Hedging a short position with long call

Investors buying call options are typically bullish on a security, or are looking hedge their short positions.

• Limited downside risk – A long call position has limited downside risk, which is the call option premium.
• Cash extraction – An investor who needs cash can sell the underlying and buy call options to maintain upside exposure to the underlying asset
• Hedging – An option can be used to hedge a short/long position in the underlying asset.

Example: Hedging a Short on the Underlying Asset

Assume the following scenario:

• An investor has short sold the underlying asset at $12.00 (s0).
• At the same time, he bought a call with a strike price of $13 (X).
• The premium paid for the call option was $1 (c).

Cash Flows:

1. Loss of (s0 – ST) when underlying rises, move against original short position.
2. –c, call premium.
3. Option payoff of Max (ST – X, 0) if call option is exercised.

To execute:

• Sell asset at s0 = $12.00
• Buy call at strike X = $13
• Pay call premium = c = $1
• Asset price @ time T = ST

Thus, Profit = Max {0, ST – X} – (ST + S0) – c

This translates into Profit= (Call Payoff) – (Movement in underlying) – Call premium

 

Scenarios:

Maximum Loss: If ST>X, prices move against original short position, exercise hedge

• Max Loss= (ST – X) – (s0 – ST) – c
• Can be simplified to: s0 – X – c
  
  

Maximum Gain: If ST<X, prices move favourably against original short position, option is not exercised

• Maximum gain: 0 + (s0 –ST) – c

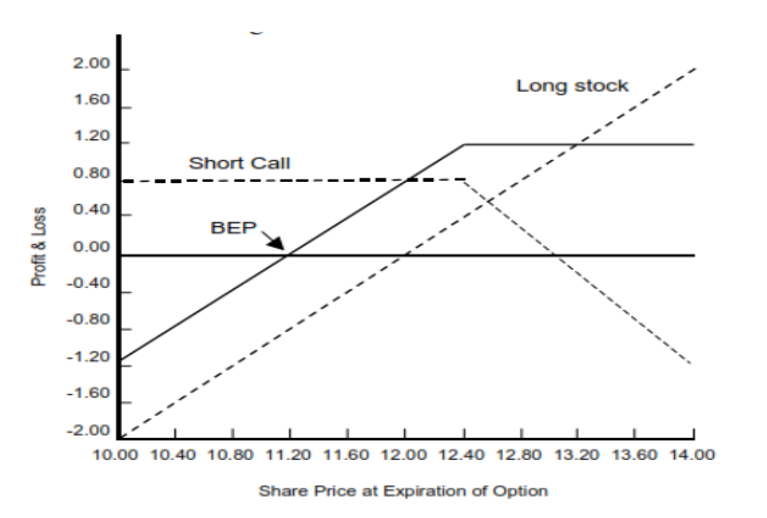
3.2. Covered Call

1. Uncovered (naked) Call: The investor only collects premium, at risk of unlimited losses if underlying asset price rallies sharply. Writer will have to purchase underlying from market at higher price to fulfil delivery obligation.
   
   
2. Covered Call: Involves the simultaneous purchase of the underlying asset with the sale of a call option. The call writer hedges his position by buying the underlying asset. Viewed as a yield enhancement

 

Example of a Covered Call

• The investor bought the underlying asset at $12.00 (s0)
• At the same time, he sold a call with a strike price of $13 (X).
• The premium received for the call option was $1 (c).
  
  

To execute a covered call strategy:

• Buy asset = s0 = $12.00
• Write call (strike) = X = $13
• Call price or premium = c = $1
• Asset price @ time T = ST

Thus, Profit = (ST – s0) – Max {0, ST- X} + c

Translates to Profit= (Long asset position) – (Option Payoff) + Call premium

 

Scenarios:

• Market in uptrend: Covered call will underperform as potential gain is limited to premiums received. Although premiums will rise if volatility is high
• Market is flat/choppy: Outperform as investor keeps the premium from selling the call option.
• Market in downtrend: outperform as they keep the premium received from selling the call option, which o‑sets some of the asset’s decline.

Maximum Gain: If ST > X, ITM, call option is exercised.

Option Writer’s Profit: (ST – s0) – (ST – X) + c

Simplified to: = X – s0 + c= $12.40 – $12.00 + $0.80 = $1.20

 

Maximum Loss: If ST ≤ X, ATM, OTM, call not exercised, max loss occurs when asset price drops to 0

Option Writer’s Profit: (ST – s0) – (ST – X) + c; ST= 0, option payoff=0

Simplified to: = -s0 + c= -$12 + $0.80= -$11.20

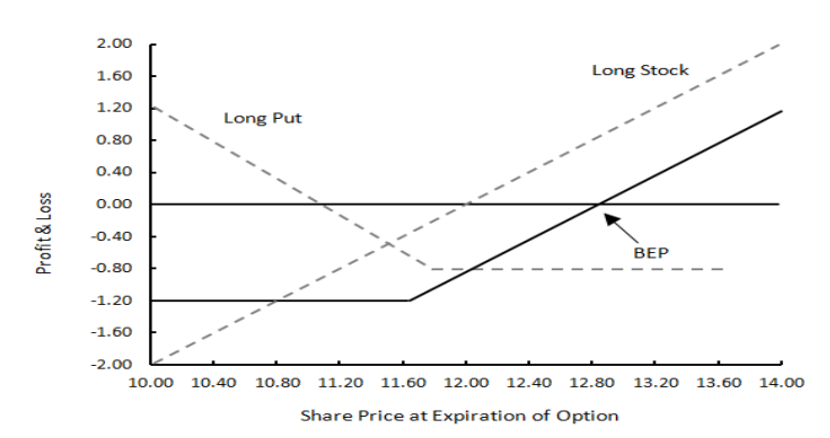
3.3. Protective Put

Typically used to take a bearish view on the underlying asset.

1. Uncovered: Similar to shorting the underlying asset. The holder will profit from a decline in the price of the underlying asset.
2. Hedging (Protective Put): Combines a long put with a long asset position. Helps limit downside while still maintaining exposure to the upside afforded by an increase in the underlying asset. However, upside is limited by option premiums.
   
   

Example of a Protective Put

• Investor has bought the underlying asset at $12.00 (s0)
• Bought a put with a strike price of $11.60 (X)
• The premium is $0.80 (p).
  
  

To execute a protective put strategy:

• Buy asset at s0 = $12.00
• Buy put at X = $11
• Pay premium = p = $1
• Asset price @ time (T) = ST (T = expiration date)

Thus, Profit = (ST – s0) + Max {0, X – ST} – p

Translates to: (Long asset position) + (Long put) – put premium

 

Scenarios:

• Market in uptrend: Unlimited upside, but Protective Put will underperform as the cost of premium paid reduces total return.
• Market in downtrend: Outperform as losses are limited to premiums paid

Maximum Gain: If ST > X, put option is not exercised

Profit = (ST – s0) + Max {0, X – ST} – p

Simplifies to: ST – s0 + 0 –p= ST – $13 (theoretically unlimited)

Maximum Loss: If ST ≤ X, put option is exercised to hedge decline in long asset position

Profit = (ST – s0) + Max {0, X – ST} – p

Simplifies to: -s0 + X – p= -$12+ $11 – $1 = -$2

 

The protective put strategy is used to provide downside protection while at the same time pursuing capital appreciation. Upside potential is unlimited, but premium paid reduces return.

 

Summary: Covered Call & Protective Put Strategies

Covered Call

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

The Covered Call strategy generates income by receiving premiums for writing the call option. In exchange for upside potential being capped, yields earned are typically better than average.

It can be a yield-enhancing alternative to traditional fixed income. At the same time, the strategy allows investors to maintain long exposure to the underlying asset.

Because option premiums tend to increase with higher volatility, covered call strategy provides investors the opportunity to benefit from rising volatility that might have a negative impact on bonds and assets.

 

Protective Put

Source: CM-SIP – Capital Markets – Specified Investment Products – Derivatives and Collective Investment Schemes (SIP)

 

By paying a premium for the put option, an investor is able to limit downside while still attain exposure to upside potential in the underlying asset. However, upside is capped due to premiums paid.